Resistance and Resistivity
Resistance it the opposition to the passage of current within a component. The Resistance of a component decides how much voltage will be dropped across it for a particular current.
Resistance is measured in Ohms (Ω). According to Ohm’s Law, voltage is the product of current and resistance. Therefore Ohms can be expressed in base units as \mathrm{Kg}\mathrm{m}^2\mathrm{s}^{-3}\mathrm{A}^{-2}.
V=IR
- Everything has Resistance, because everything has some opposition to the flow of Electric Charge. Components whose sole purpose is to provide a Resistance of a certain value are called Resistors.

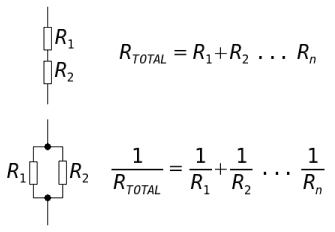
- When Resistors are connected in Series, the total Resistance across them will be equal to the sum of each Resistor value. The total voltage will be equal to the sum of the voltages across each Resistor. This rule will also apply for other components.
- When Resistors are connected in Parallel, the reciprocal of the total resistance will be equal the sum of the reciprocals of each Resistor Resistance. The total voltage dropped will be the same as the voltages dropped across all the individual Resistors.
Resistivity
Resistance is a Sample Constant, so is specific to individual components. However, there is a Material Constant that can be used to find the Resistance of any component of a specific material. This is Resistivity. Together with the length and cross-sectional area of a sample, it can calculate its resistance.
Resistivity is given the symbol ρ and is measured in Ohm Meters (Ωm, or Kgm3s-3A-2 in base units).
For example, copper has a Resistivity of 1.68 ×10-8 Ωm, and Germanium 4.6 ×10-1 Ωm.
The Resistance of a material of Resistivity ρ, length l and cross-sectional area A is calculated by the formula: