Hooke’s Law
Hooke’s Law states that, for certain elastic materials, force is proportional to extension, when a sample is stretched. This means that the extension of the sample increases linearly with the amount of force applied. Materials that obey Hooke’s law are called Hookean Materials. Springs behave like Hookean Materials.
Hooke’s law can be written as F = kx, where F is Force, x is extension, and k is the Stiffness Constant of the sample. The stiffness constant describes the stiffness of a material, and is measured in Nm^{-1} (or Kgs^{-2}).
F = kx
- Hooke’s law can be demonstrated with the use of Force-Extension graphs.

- However, no sample follows Hooke’s law indefinitely, and there comes a point, called the Limit of Proportionality, where there is no longer a linear relationship between force and extension. After yet more force is applied, the Elastic Limit will be reached. This means that the sample will no longer return to its original shape when the force ceases to be present. Eventually, the force will become so great that the material snaps. This is called the Yeild Point.
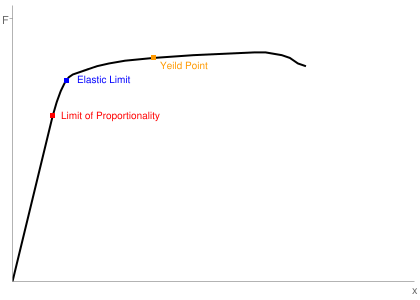
Before the elastic limit is reached, the sample is experiencing Elastic Deformation, where it will return to its original shape when the load (force) has been removed. However, once the material passes that point, it experienced Plastic Deformation, where its shape is permanently changed.
If two springs are used in series, the effective stiffness constant of both of them is less than either of them. In fact, it can be worked out by the formula: \frac{1}{k_{\text{eq}}} = \frac{1}{k_1} + \frac{1}{k_2}. If two springs are in parallel, their effective stiffness constant is greater: k_{\text{eq}} = k_1 + k_2.